Mit Ökonometrie kann man wunderbar Erkenntnisse gewinnen, wunderbar rumspielen und wunderbar manipulieren. Eine Einführung.
Letzte Woche sprach ich mit einer guten Freundin, die an ihrer Dissertation in Volkswirtschaftslehre arbeitet. Ich weiß nicht wie, aber wir kamen auf berufliche Klischees, landläufige Vorstellungen von Berufsbildern, ich berichtet von jener Hochzeit, bei der meine unglückliche Schwester Lakritzbonbons in ihrem Essen fand, während ich der Sitznachbarin erklären durfte, wo eigentlich der Unterschied zwischen Betriebs- und Volkswirtschaftslehre ist. Die Freundin wiederum konnte berichten, daß es auch in ihrem Heimatumfeld (ähnlich provinziell wie meines) zu manchem Mißverständnis käme. Sage man nämlich, man promoviere in Volkswirtschaftslehre, stellt sich automatisch das Bild von einem Büro mit vielen Büchern und Aufsätzen ein. Das ist natürlich teilweise richtig, aber wenn diese Freundin dann sagt, daß sie das erste Jahr ausschließlich Statistik und Mathematik gelernt hat, ist die Überraschung groß. Jeder kennt zwar einen Sohn oder eine Tochter von Bekannten, die sich in der Pflichtvorlesung Mathematik im BWL-Studium sehr schwer getan hat. Daß allerdings in den USA ein wesentlicher Teil der Doktoranden in Economics einen Master-Abschluß in Physik oder Mathematik mitbringt aber keinerlei Grundkenntnisse in Wirtschaft ist eine hierzulande ungeahnte Dimension . Ich erinnere mich an einen Abgänger einer renommierten Privathochschule für Wirtschaftswissenschaften, der als Jahrgangsbester dennoch keinerlei Chance hatte, in den Doktoratsstudiengang einer ähnlich renommierten Hochschule der USA aufgenommen zu werden: seine Mathekenntnisse seien dafür keinesfalls ausreichend.
Genau das ist jedoch die Realität, die möglicherweise nicht ganz unbeteiligt daran ist, daß die Welt blinden Auges in eine Finanzkrise erster Güte geschlittert ist: in den Wirtschaftswissenschaften wird die vorwiegend auf Worte gestützte Analyse zumeist belächelt. Wer nicht mit Modellen und quantitativen Analysen aus der Rechenmaschine aufwarten kann (mit Ergebnissen, die von Hand durchzurechnen ein Mensch Jahre bräuchte) gilt nicht viel. Ein wesentlicher Teil der Forschung wie auch der politikberatenden Zunft konzentriert sich auf höhere Mathematik, die für den Laien nur schwer einzuordnen ist.
Die Grundlagen hingegen sind recht simpel. Wenn man Statistik der Sorte „Grundstudium Wirtschaftswissenschaften” mit Mathematik auf Abiturniveau kombiniert, kann man viel Spaß haben. Man kann nämlich mittels der Regressionanalyse alle möglichen Zusammenhänge zwischen zwei verschiedenen Faktoren herstellen, solange man nur beide irgendwie messen oder quantifizieren kann.Das Grundprinzip ist einfach und auch für weniger mathematikaffine Personen zu begreifen.
Man nehme zwei Variablen, sagen wir: Demokratie und Bruttosozialprodukt. Das Bruttosozialprodukt ist ohnehin schon eine Zahl. Demokratie ist natürlich keine Zahl, aber fleißige Wissenschaftler haben Informationen über die Qualität von Demokratien gesammelt und diese systematisch in ein Ranking umgearbeitet, so daß daraus auch eine Zahl wird. Zwei Zahlen kann man leicht auf einem Graphen abbilden und erhält eine Wolke von Punkten: jedes Land ein Punkt. Dann sagt man dem Computer: Errechne eine Linie, die möglichst genau auf die Punktewolke passt. Man muß dem Computer natürlich noch mitteilen, was genau passend ist, und die gängigste Methode ist die „kleinste Quadrate Methode”. Die Linie bildet den durchschnittlichen y-Wert für jeden x-Wert ab (im Beispiel also das durchschnittliche [BIP-Wachstum] für jedes Demokratieniveau) und mit der genannten Methode werden die Abstände zwischen den tatsächlichen und den rechnerischen Werten minimiert (präziser: die Quadrate der Abstände werden minimiert).
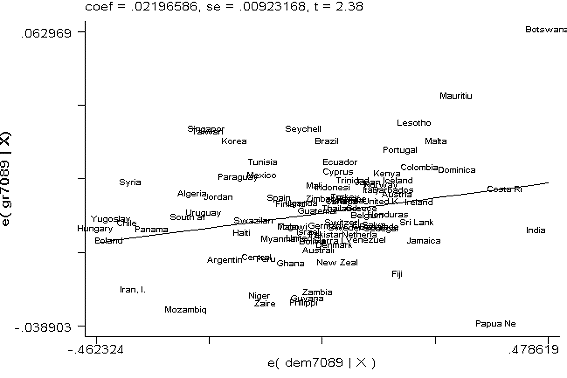
Graphik: Dani Rodrik für den IMF, 1999.
Das ist nun keine ganz große Überraschung, daß Demokratie und höheres Wachstum miteinander einhergehen und über Kausalität sagt die Regressionsanalyse in dieser Form auch nichts aus – es ist im Zweifel nur eine robuste Korrelation. Was im zweidimensionalen Raum funktioniert, geht allerdings auch mit erheblich mehr Variablen und dann wird es spannend. Unter bestimmten Voraussetzungen kann man den Ergebnissen ablesen, ob sich Faktoren positiv oder negativ auswirken, welche Bedeutung sie im Vergleich haben und im besten Falle kann man tatsächlich auch kausale Zusammenhänge bestimmen. Das allerdings ist nicht ganz einfach. Bei Fragen wie zum Beispiel Demokratie und Wachstum sind intuitiv beide Richtungen denkbar: demokratische Länder wachsen schneller, aber reiche Länder können sich auch bessere Demokratien leisten – dieser Zusammenhang gilt denn auch nach wie vor als umstritten. Solchen Problemen und allerlei anderen, die mit der Art der Daten zutun haben, versucht man einerseits durch immer kompliziertere mathematische Verfahren beizukommen. Siehe oben.
Das andere ist die „credibility revolution” in der empirischen Wirtschaftsforschung. Das hört sich aufregend an: Revolution, Glaubwürdigkeit, ich erwartete große Erkenntnisse. Die Waffen dieser Revolution waren jedoch nicht Gewehre und Kanonen, sondern spitze Federn, Computer und kluge Gedanken. Vor zwanzig Jahren wurde ebenfalls bereits mit solchen Methoden geforscht – allerdings glaubt kaum jemand die Schlußfolgerungen, zu groß war die Unsicherheit, zu instabil die Ergebnisse. Neben Fortschritten im mathematischen Verständnis wird allerdings heute vor allem mehr wert auf gutes „research design” gelegt – also darauf, daß die Daten, Fragestellung und Methoden eine sinnvolle Allianz eingehen.
Dazu gehört ein großes Augenmerk auf zufällig zusammengestellte Daten ohne Selektionseffekte – also systematische Unterschiede beim Vergleich von Gruppen, die die Ergebnisse verzerren wie auch der gesamte Aufbau der Studie. Manchmal liegt die Lösung nämlich darin, das richtige Beispiel zu finden, an dem man eine Hypothese testen kann. Oder den Einsatz einer auf den ersten Blick völlig unsinnigen Variable, die das Problem der gegenseitigen Beeinflussung löst.
Zum Beispiel haben sich einige Forscher damit beschäftigt, ob Armut zu Bürgerkriegskonflikten führt. Auch das ist ein klassischer Fall von „reverse causality” und die treibenden Faktoren so komplex, daß ein simples mathematisches Modell sie nicht mehr auseinanderdividieren kann. Die Forscher nutzen nun folgende Argumentation: Armut führt zu Bürgerkrieg und Bürgerkrieg zu Armut – mit diesen zwei Variablen erhält man daher keine Antwort. In landwirtschaftlich orientierten Volkswirtschaften hängt Armut jedoch mit Regen zusammen: viel Regen sorgt für gute Ernten, wenig Regen für schlechte Ernten. Schlechte Ernten wiederum führen zu Armut – und umgekehrt. Andererseits hat Regen mit Bürgerkrieg wenig zu tun und ein kausaler Zusammenhang ist unwahrscheinlich. Wenn nun folglich wenig Regen (und daher schlechte Ernten und Armut) mit mehr Bürgerkriegen zusammenfällt, kann man davon ausgehen, daß tatsächlich Armut zu Bürgerkriegen führt. Genauer gesagt finden die Autoren, daß eine Verringerung der Wachstumsrate des BIP um 5 % zu einer 10 % höheren Wahrscheinlichkeit von Bürgerkriegen führt. Methodisch ist es ein simpler Kniff – man muß nur darauf kommen, eine passende instrumentelle Variable zu finden. Und dann konsequent von einem Schritt zum nächsten die Zusammenhänge durchargumentieren und natürlich die jeweiligen Korrelationen nachweisen, in diesem Fall zwischen Regen, Ernten und Armut.
Das muß man natürlich nicht glauben, aber interessant ist es allemal. Trotzdem schadet es nie, eine gesunde Skepsis gegenüber statistischen Studien zu bewahren: Daten sind immer manipulierbar, und selbst die beste Studie kann im Ergebnis von den Lesern und Intermediären verdreht werden – zumal wenn diese eine politische Agenda haben. Im Zweifel sollte man immer zur Originalstudie zurückgehen, da kann zumindest niemand Korrelation und Kausalität durcheinanderbringen.